Turbo码发展历史

• 　　Shannon 编码定理指出：如果采用足够长的随机编码，就能逼近Shannon 信道容量。但是传统的编码都有规则的代数结构，远远谈不上“随机”；同时，出于译码复杂度的考虑，码长也不可能太长。所以传统的信道编码性能与信道容量之间都有较大的差距。事实上，长期以来信道容量仅作为一个理论极限存在，实际的编码方案设计和评估都没有以Shannon限为依据。

  　　1993 年两位法国教授Berrou、Glavieux 和他们的缅甸籍博士生Thitimajshima 在ICC 会议上发表的Near Shannon limit error-correcting coding and decoding: Turbo codes”，提出了一种全新的编码方式——Turbo 码。它巧妙地将两个简单分量码通过伪随机交织器并行级联来构造具有伪随机特性的长码，并通过在两个软入/软出(SISO)译码器之间进行多次迭代实现了伪随机译码。

  　　仿真结果表明，在AWGN 信道下，码率为1 2 的Turbo 码在达到误比特率(BER) ≤ 10?5时， 0 E N b 仅为约0.7dB (这种情况下达到信道容量的理想0 E N b 值为0db)，远远超过了其他的编码方式，一时在信息和编码理论界引起了轰动。

  　　从此以后，Turbo 码得到了广泛的关注和发展，并对当今的编码理论和研究方法产生了深远的影响，信道编码学也随之进入了一个新的阶段。

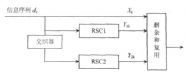
  　　Turbo码由于其近Shannon界的突出纠错能力，成为近年信道编码理论研究的热点问题。其编码器由两个（或多个）带反馈的系统卷积码器经一交织器并行级联而成，接收端一般采用逐位最大后验概率译码器通过反复迭代循环来译码。